
線分の一端から任意の角度で線分を引く
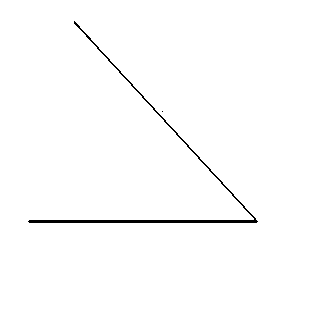
コンパスで3回同じ長さを書く
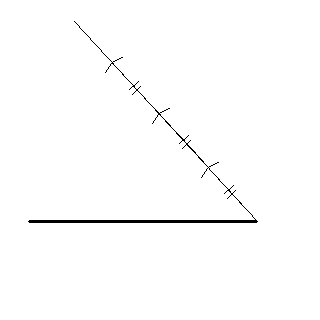
元の線分をAB、新たな点をC,D,Eとする。
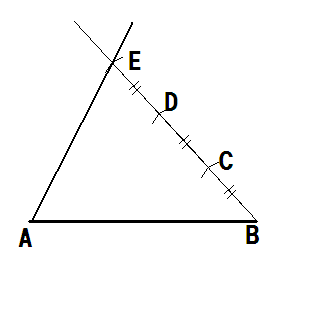
AEを結び基準せんとする
D、Cから本当は三角定規二つ使って、平行線を書く
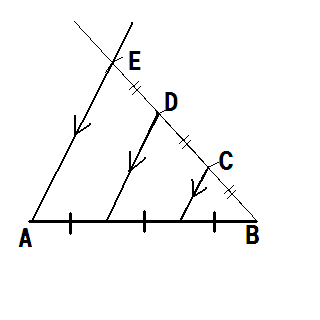
今回の設定の場合、三角定規が入っていないので、 Eから適当な半径で弧を描きF,Gとする 同じ半径でD点から弧を描きHだけ決まる FGの長さをコンパスで写し取り Hから弧を描けば交点からiが求められる Diを結べばEAと平行線になる
同じことをCで行なえば
出来上がり
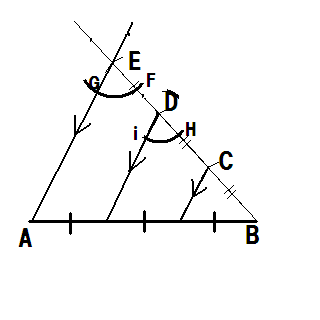
試験場には「三角定規が持ち込めないので、
「コンパスだけ」で作る作図法を紹介
斜辺に3等分の印を付ける時に、コンパスを3回使いましたね。
その半径のままで、E点とD点、および、E点からの円と線分AEの交点からの3つの弧を描くと
最終的に、4つの点でできる四角形EFGDが出来ます。
四角形EFGDは、4辺の長さが等しいので「ひし形」ですから、EF//DGで、「平行線」が描けるのです。


最後に、G点からと、C点から円を描き、点Hを見つければ、
平行線が2本見つかり、
本当の「三等分」の完成です。
