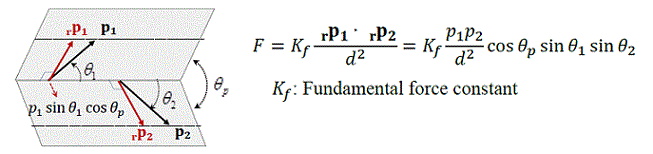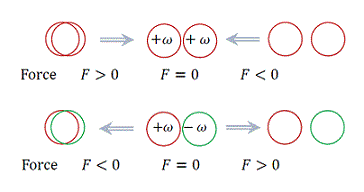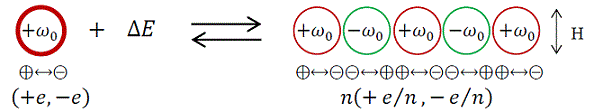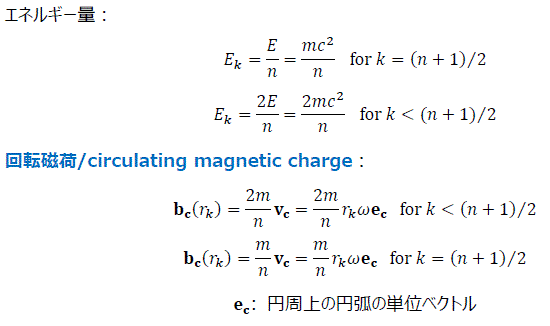はじめに ー 目次
目 次
- はじめに -----<エネルギー周回理論>-------
- エネルギーとは何だろう?
- 内在エネルギーと質量
- エネルギー間に働く力
- 基本力とエネルギー周回
- エネルギー周回間の相互作用
- 初期宇宙からの宇宙分離
- 4次元球3次元球面の宇宙空間
- 空間エネルギーとスペーシア
- 見かけエネルギーの伝搬
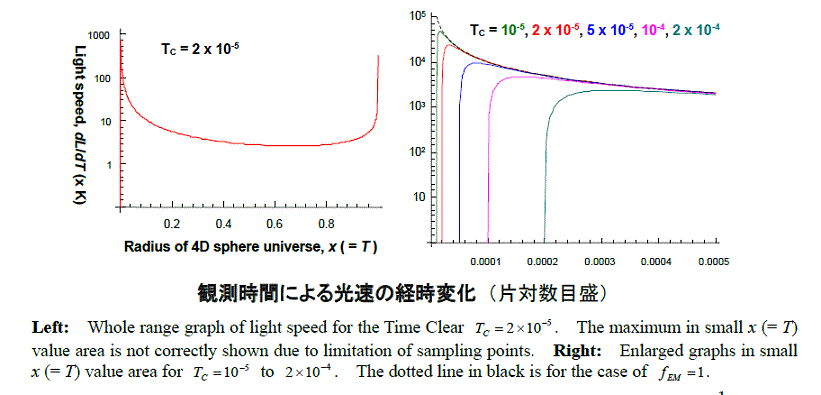
- 基本定数と光速の経時変化
- 宇宙膨張は加速していない
- 現代物理迷走の始まり
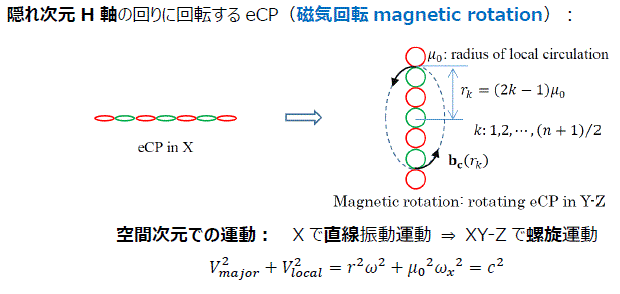
- 隠れ次元での運動量
- 電荷と電気力
- 隠れ-空間次元周回 iS の伸長
- 伸長周回 n-iS の回転
- 光について
- 基本周回と量子粒子
- 中性子の構造と安定性
- 中性子のβ崩壊:陽子と電子の生成
- 実空間での位置を示す波動関数
- エネルギー周回の軌道周回運動
- 波動関数の特徴と軌道周回の波動関数
- 原子中の電子のエネルギー
- 原子軌道の量子化と半径
- S軌道とP軌道の波動関数
- 波動関数を与える波動方程式
- シュレーディンガー方程式の矛盾
- 新しい量子力学のまとめ
- 既存量子力学の問題点
- 不確定性原理の虚構
- 早期宇宙周回の分離と環状分解
- 銀河種のエネルギー表示
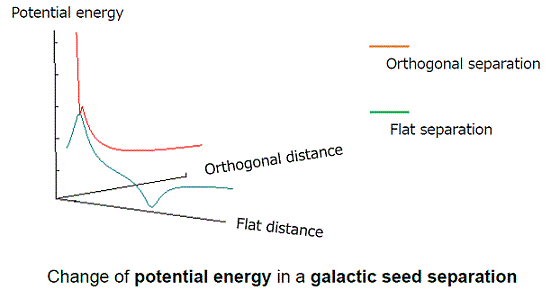
- 銀河種の分離
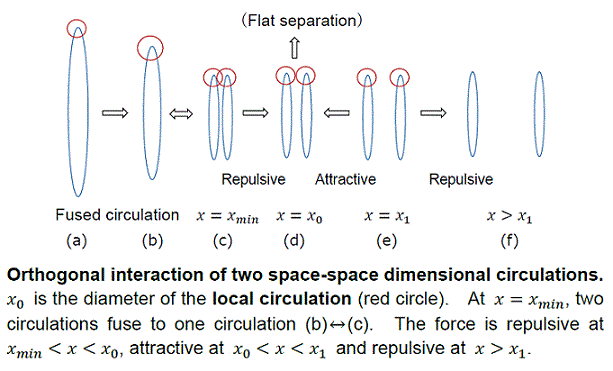
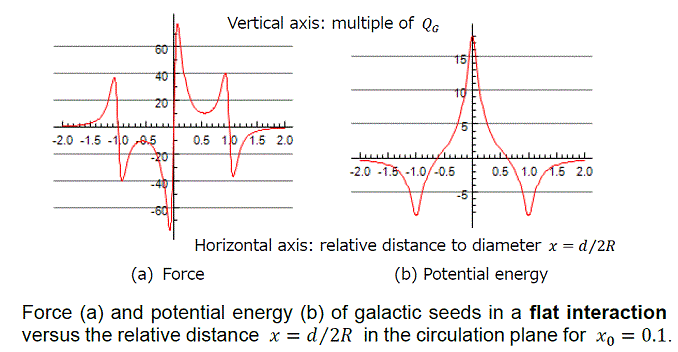
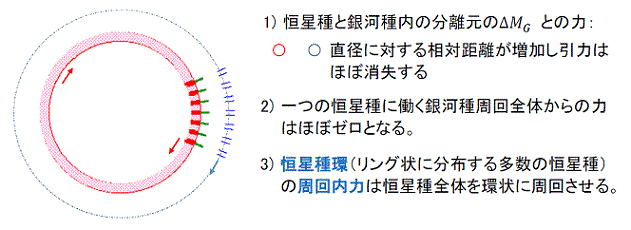
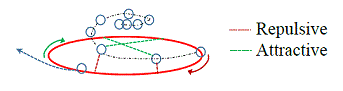
- 銀河種の水平相互作用
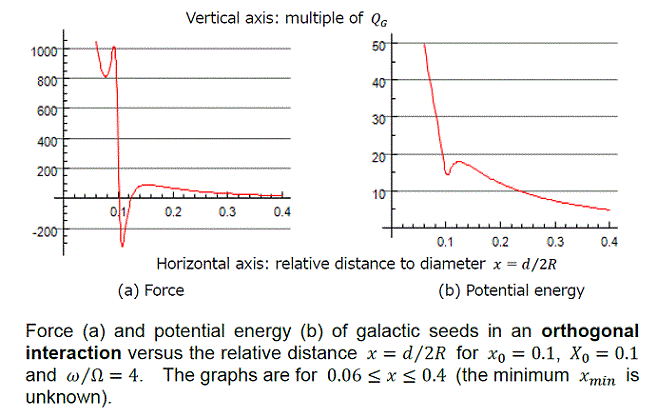
- 銀河種の垂直相互作用
- 銀河種分離に伴うエネルギー放射
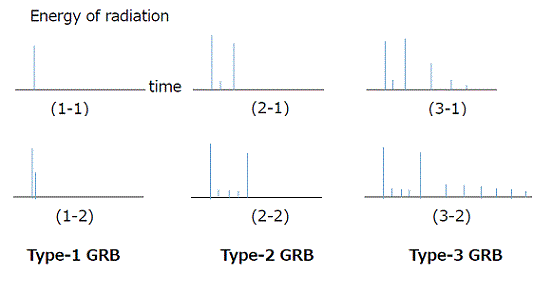
- ガンマ線バースト
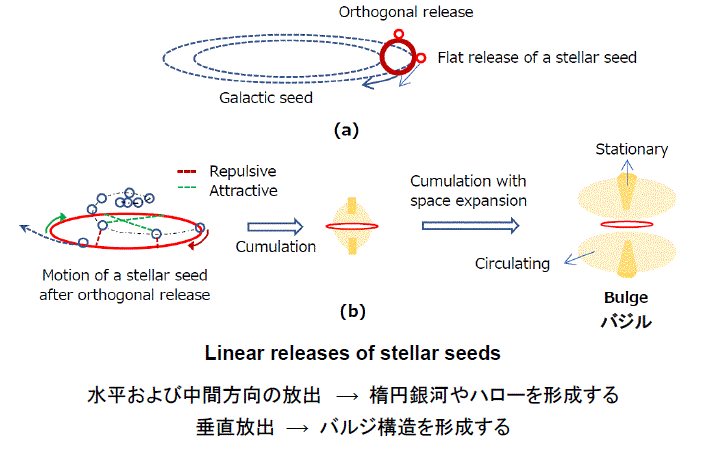
- 銀河種からの恒星種の放出
- 銀河渦巻円盤での星の周回速度
- 宇宙マイクロ波背景放射
- エネルギー周回理論と標準宇宙論
- 空間エネルギーと見かけエネルギーへの分割
- 光速の経時変化1:時間
- 光速の経時変化2:光速を示す数式
- 赤方偏移
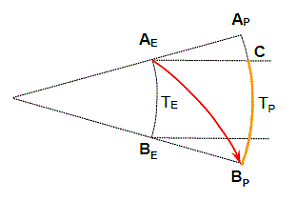
- 光伝搬距離と現在距離
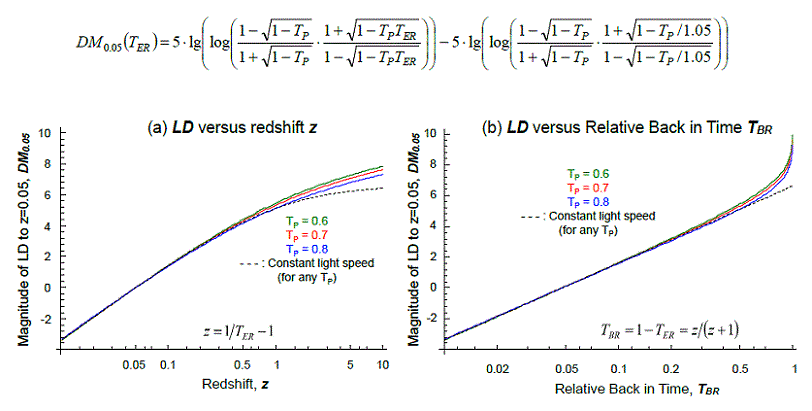
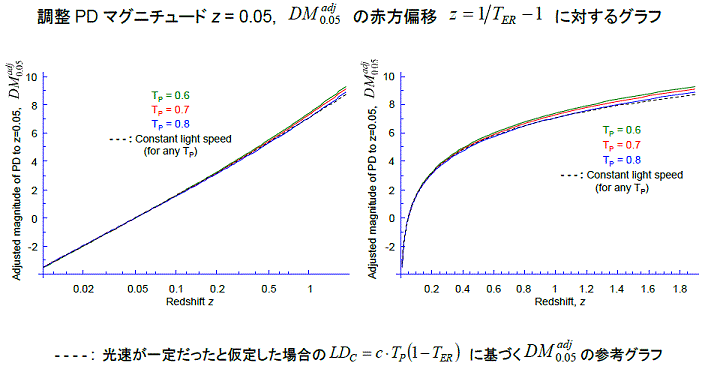
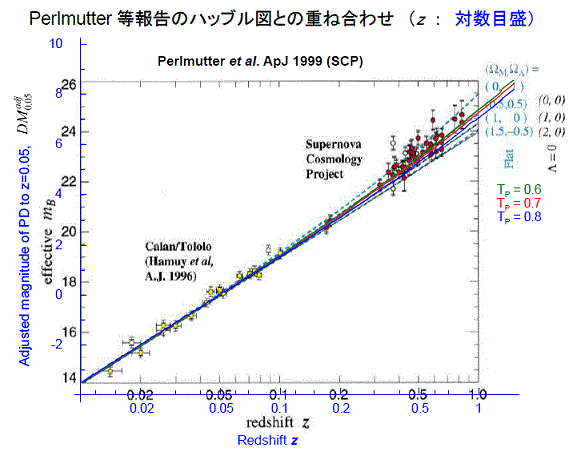
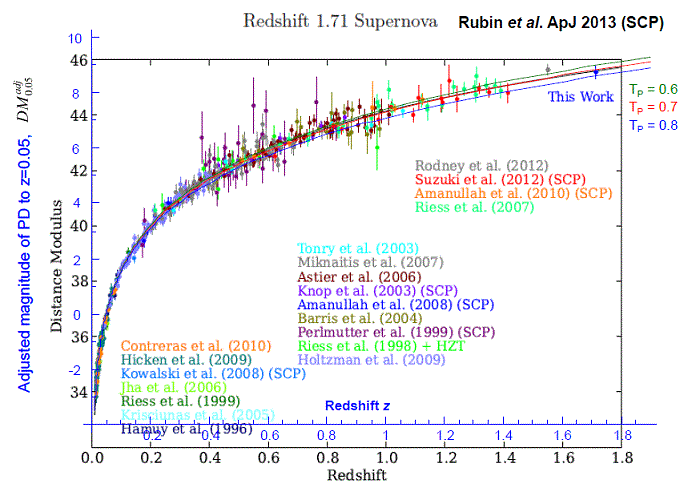
- ハッブル図1:距離指数
- ハッブル図2:K補正
- 超新星実測値と理論値のハッブル図
- 孤立電荷および静電力は存在しない
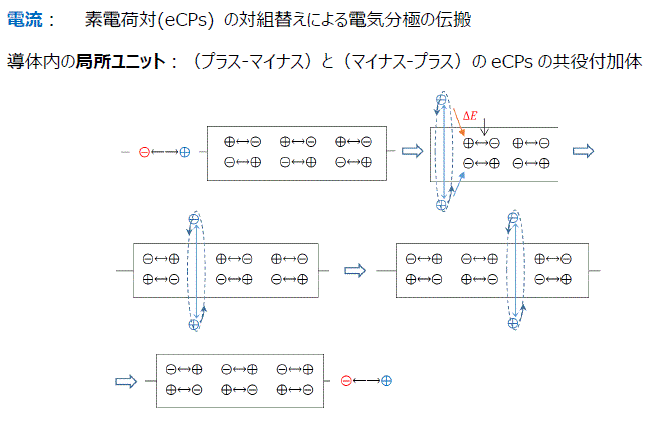
- 電流とは何か
- 分極エネルギー伝搬のモデル
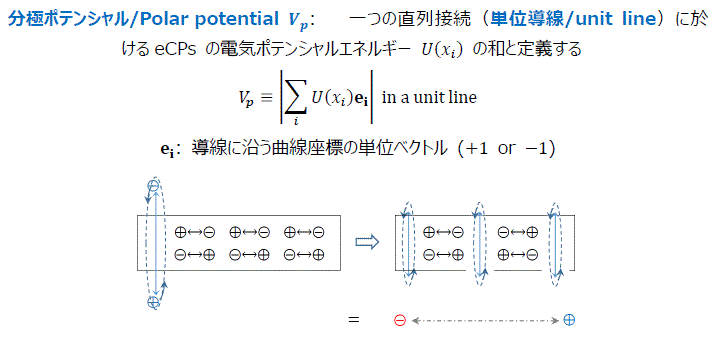
- 分極ポテンシャル
- 電流の定義
- 電流ポテンシャル
- 既存電磁気学との比較
- 磁荷
- 磁荷密度
- 電流に伴う回転磁荷
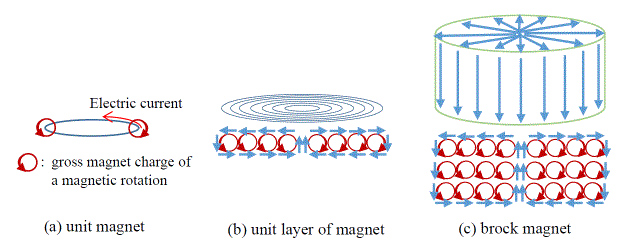
- 磁石
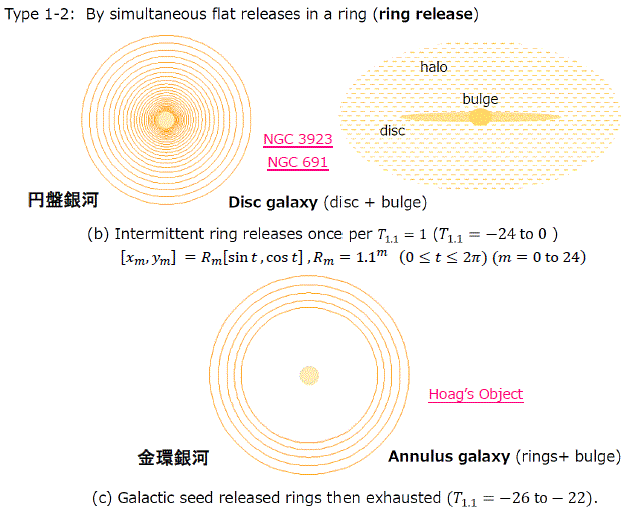
- 銀河形状の形成:銀河種の種類
- 恒星種放出の種類
- 単独銀河種-環状放出
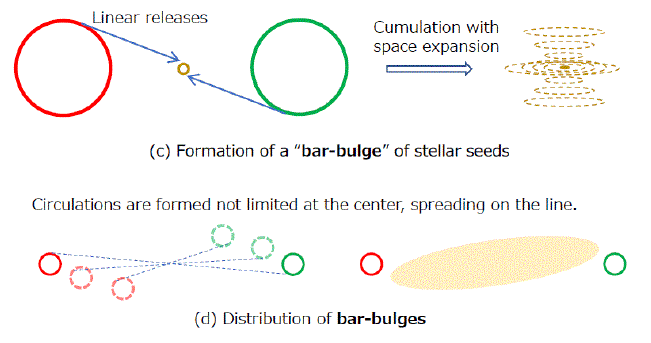
- 回転二連銀河種-バーバルジの形成
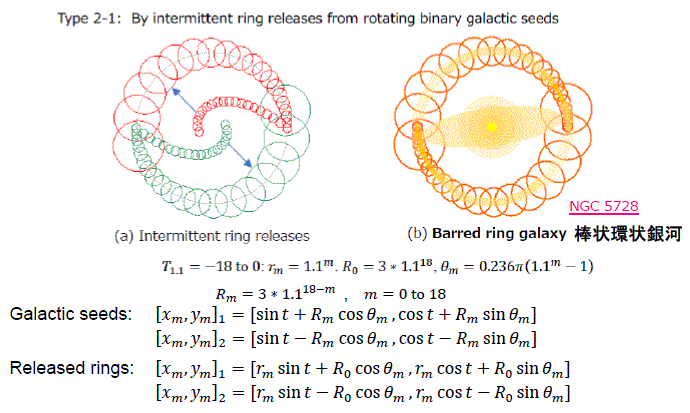
- 回転二連銀河種-環状放出
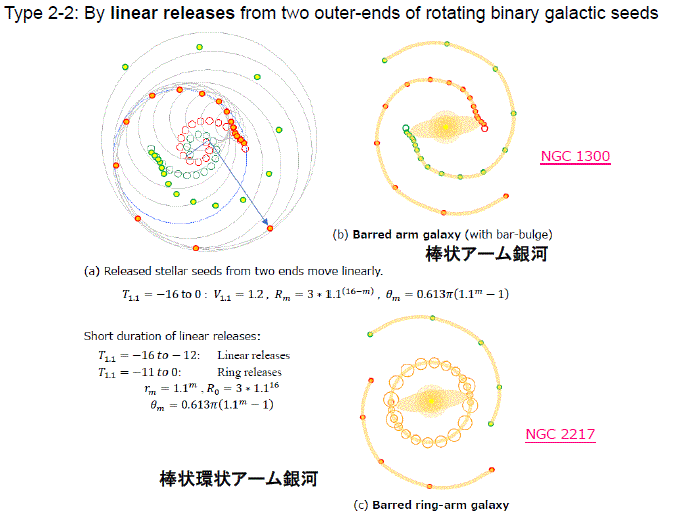
- 回転二連銀河種-外端直線状放出
- 隣接銀河種-環状放出
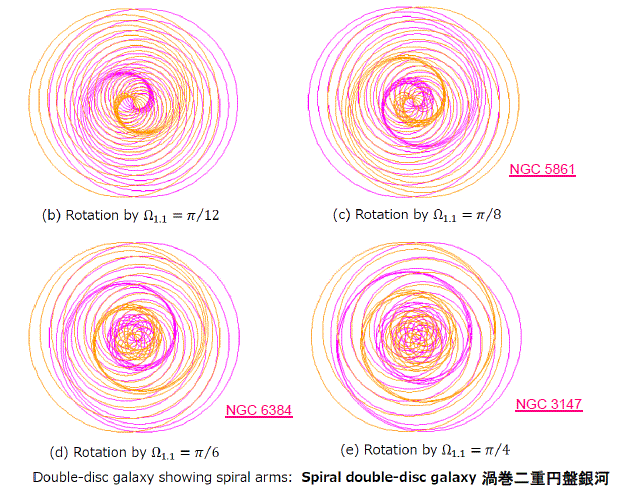
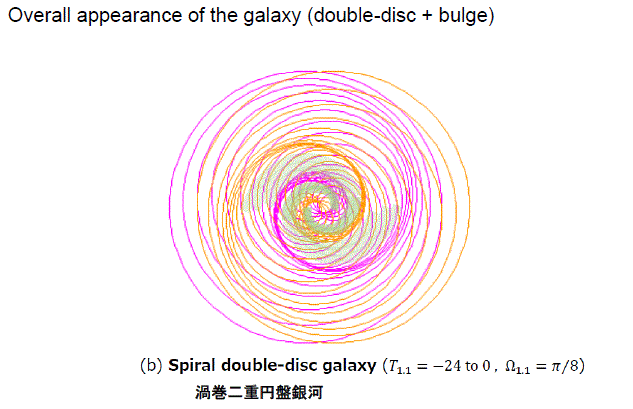
- 渦巻二重円盤銀河のバルジ
- 隣接から二連に変化する回転銀河種-環状放出
-----<ECTからの宇宙概略>-------
-----------<粒子>--------------
---------<量子力学>------------
---------<宇宙進展>------------
---------<ハッブル図>-----------
---------<電磁気学>------------
-------<銀河形状の生成>---------
物理学では、ある法則が提案されそこから数学的、論理的に誘導される内容が実測結果と合致すればその法則は正しいはずとされる。ここには落し穴がある、法則が定義された要素で成り立っているかどうかだ。例えば、ニュートンの万有引力の法則では二つの質量間に働く力を与える。しかし質量は定義されているだろうか。ニュートンの運動法則は力が質量に与える加速度を示す。質量はこの運動法則により力と加速度の実測値から得られる。実は質量は定義されたものではなく、二つの法則の間で自己循環している。一方、相対性理論では質量とエネルギーの等価性がうたわれている。しかし、エネルギーも一義的には定義されておらず、質量、加速度、力などから2次的に誘導されている。
質量やエネルギーは何となく我々が概念している内容が法則の要素と推測される。従ってこれらの法則は現実の物理事象を示すだろうと推測される。しかし、粒子崩壊などでは最初の粒子状態を未定義の要素で記載している。崩壊した後の状態を同類の要素で記載し、この崩壊過程を規定する力やポテンシャルの法則を提起し、実験結果を導けるのでこの法則は正しいとしている。実はこれは本末転倒で、実験結果が導かれるように法則を得ている。もし状態を規定する要素が実在するものであれば物理的に意味がある。しかし、全く空想的要素を規定すれば、そこから導く法則は、例え数学的に可能てあっても物理法則としてはあり得ないものとなる。
既存の標準物理では未解決な重大問題が余りにも多すぎる。暗黒物質、暗黒エネルギーだけでなく渦巻銀河の形成やガンマ線バーストも説明できない点が多くある。既存概念を一旦脱ぎ捨て、最初の出発点となる要素の定義から始めて物理法則を考えよう。